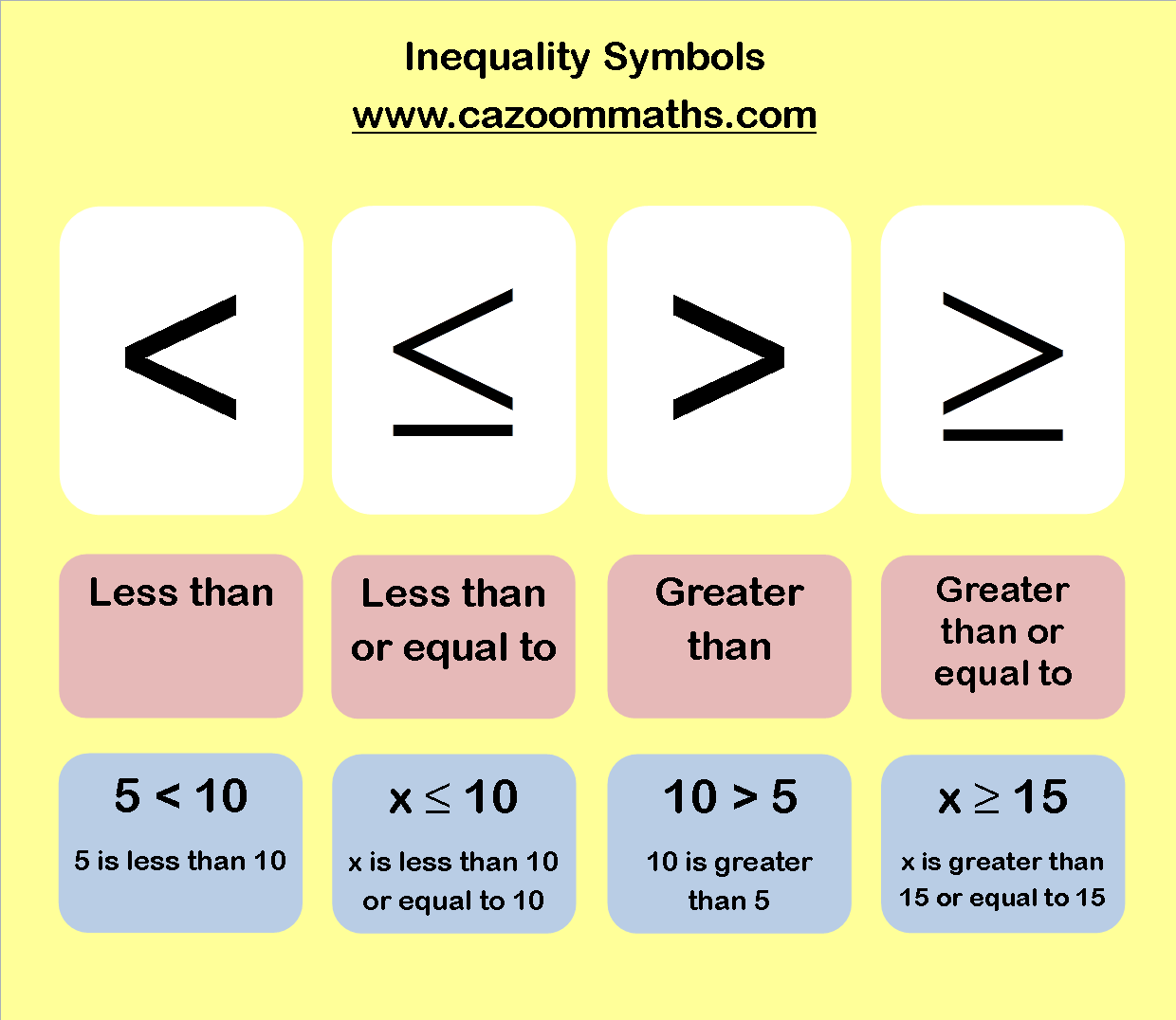Inequalities Chart
Inequalities Chart - Operations on linear inequalities involve addition,. Inequalities are mathematical expressions that show the relationship between two values when they are not equal i.e., one side can be greater or smaller than the other. You will work through several examples of how to solve an. If we subtract 3 from both sides, we get: A > b if and only if a − b > 0. How to solve and graph a polynomial inequality including compound, quadratic, absolute value, and rational inequalities with examples. Finally, we see how to solve inequalities that involve absolute values. An inequality is a mathematical statement that compares two expressions using the ideas of greater than or less than. Inequalities word problems require us to find the set of solutions that make an inequality. Inequalities are used to compare numbers and determine the range or ranges of values that satisfy the conditions of a given variable. How to solve and graph a polynomial inequality including compound, quadratic, absolute value, and rational inequalities with examples. Finally, we see how to solve inequalities that involve absolute values. A > b if and only if a − b > 0. If we subtract 3 from both sides, we get: You will work through several examples of how to solve an. Unlike equations, inequalities provide a range of possible values that satisfy specific conditions. We can often solve inequalities by adding (or subtracting) a number from both sides (just as in introduction to algebra), like this: Inequalities word problems require us to find the set of solutions that make an inequality. We may add the same number to both sides of an. Inequalities are mathematical expressions that show the relationship between two values when they are not equal i.e., one side can be greater or smaller than the other. If we subtract 3 from both sides, we get: You will work through several examples of how to solve an. We may add the same number to both sides of an. Operations on linear inequalities involve addition,. We can often solve inequalities by adding (or subtracting) a number from both sides (just as in introduction to algebra), like this: On the basis of this definition, we can prove various theorems about inequalities. Operations on linear inequalities involve addition,. We may add the same number to both sides of an. If we subtract 3 from both sides, we get: You will work through several examples of how to solve an. How to solve and graph a polynomial inequality including compound, quadratic, absolute value, and rational inequalities with examples. We may add the same number to both sides of an. You will work through several examples of how to solve an. Operations on linear inequalities involve addition,. Learn the process of solving different types of inequalities like linear. A > b if and only if a − b > 0. Operations on linear inequalities involve addition,. Unlike equations, inequalities provide a range of possible values that satisfy specific conditions. An inequality is a mathematical statement that compares two expressions using the ideas of greater than or less than. Inequalities word problems require us to find the set of. You will work through several examples of how to solve an. Operations on linear inequalities involve addition,. We can often solve inequalities by adding (or subtracting) a number from both sides (just as in introduction to algebra), like this: An inequality is a mathematical statement that compares two expressions using the ideas of greater than or less than. We may. Inequalities are used to compare numbers and determine the range or ranges of values that satisfy the conditions of a given variable. Operations on linear inequalities involve addition,. Learn the process of solving different types of inequalities like linear. Finally, we see how to solve inequalities that involve absolute values. Inequalities word problems require us to find the set of. You will work through several examples of how to solve an. We can often solve inequalities by adding (or subtracting) a number from both sides (just as in introduction to algebra), like this: Special symbols are used in these statements. Unlike equations, inequalities provide a range of possible values that satisfy specific conditions. Inequalities are mathematical expressions that show the. A > b if and only if a − b > 0. Inequalities word problems require us to find the set of solutions that make an inequality. On the basis of this definition, we can prove various theorems about inequalities. We can often solve inequalities by adding (or subtracting) a number from both sides (just as in introduction to algebra),. Special symbols are used in these statements. How to solve and graph a polynomial inequality including compound, quadratic, absolute value, and rational inequalities with examples. Inequalities are mathematical expressions that show the relationship between two values when they are not equal i.e., one side can be greater or smaller than the other. An inequality is a mathematical statement that compares. Inequalities are used to compare numbers and determine the range or ranges of values that satisfy the conditions of a given variable. How to solve and graph a polynomial inequality including compound, quadratic, absolute value, and rational inequalities with examples. If we subtract 3 from both sides, we get: Operations on linear inequalities involve addition,. Special symbols are used in. Finally, we see how to solve inequalities that involve absolute values. Inequalities are mathematical expressions that show the relationship between two values when they are not equal i.e., one side can be greater or smaller than the other. We may add the same number to both sides of an. You will work through several examples of how to solve an. Special symbols are used in these statements. A > b if and only if a − b > 0. Inequalities are used to compare numbers and determine the range or ranges of values that satisfy the conditions of a given variable. Inequalities word problems require us to find the set of solutions that make an inequality. If we subtract 3 from both sides, we get: Unlike equations, inequalities provide a range of possible values that satisfy specific conditions. Operations on linear inequalities involve addition,. We can often solve inequalities by adding (or subtracting) a number from both sides (just as in introduction to algebra), like this:Algebra Inequalities Math Anchor Chart
Graphing Inequalities on a Number Line Worksheet Freebie Finding Mom
My Math Resources Graphing Inequalities Poster
Inequalities Cuemath
Inequality Sign Chart
My Math Resources Graphing Inequalities Poster Bulletin Board & Anchor Chart Math
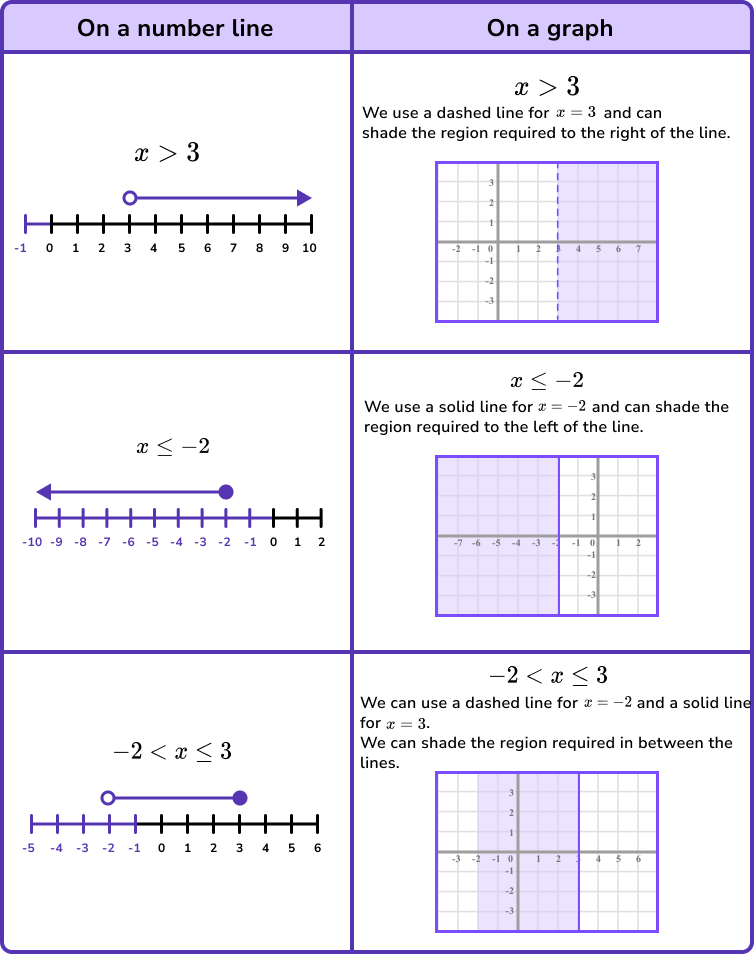
Inequalities On A Graph GCSE Maths Steps, Examples & Worksheet
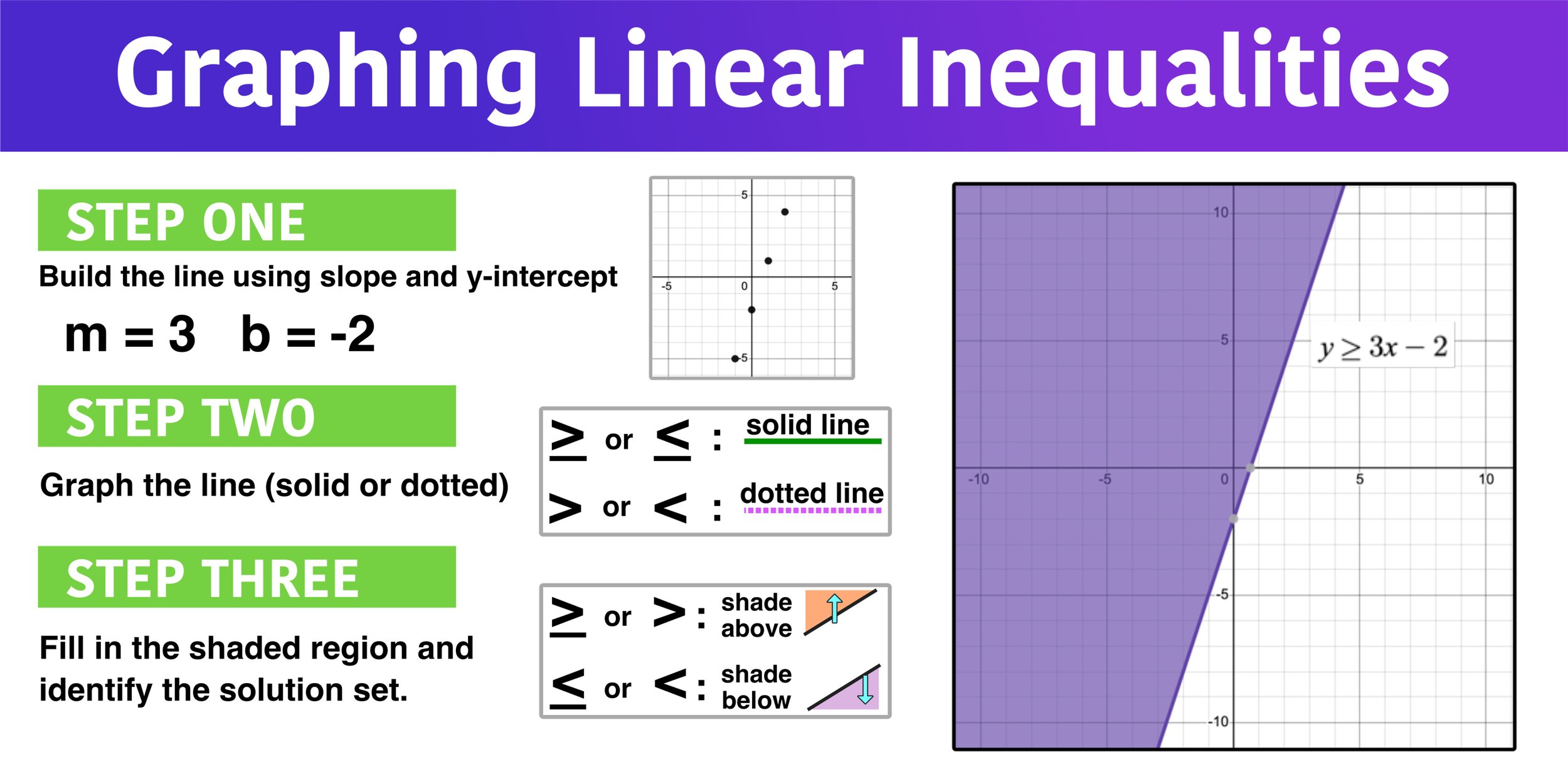
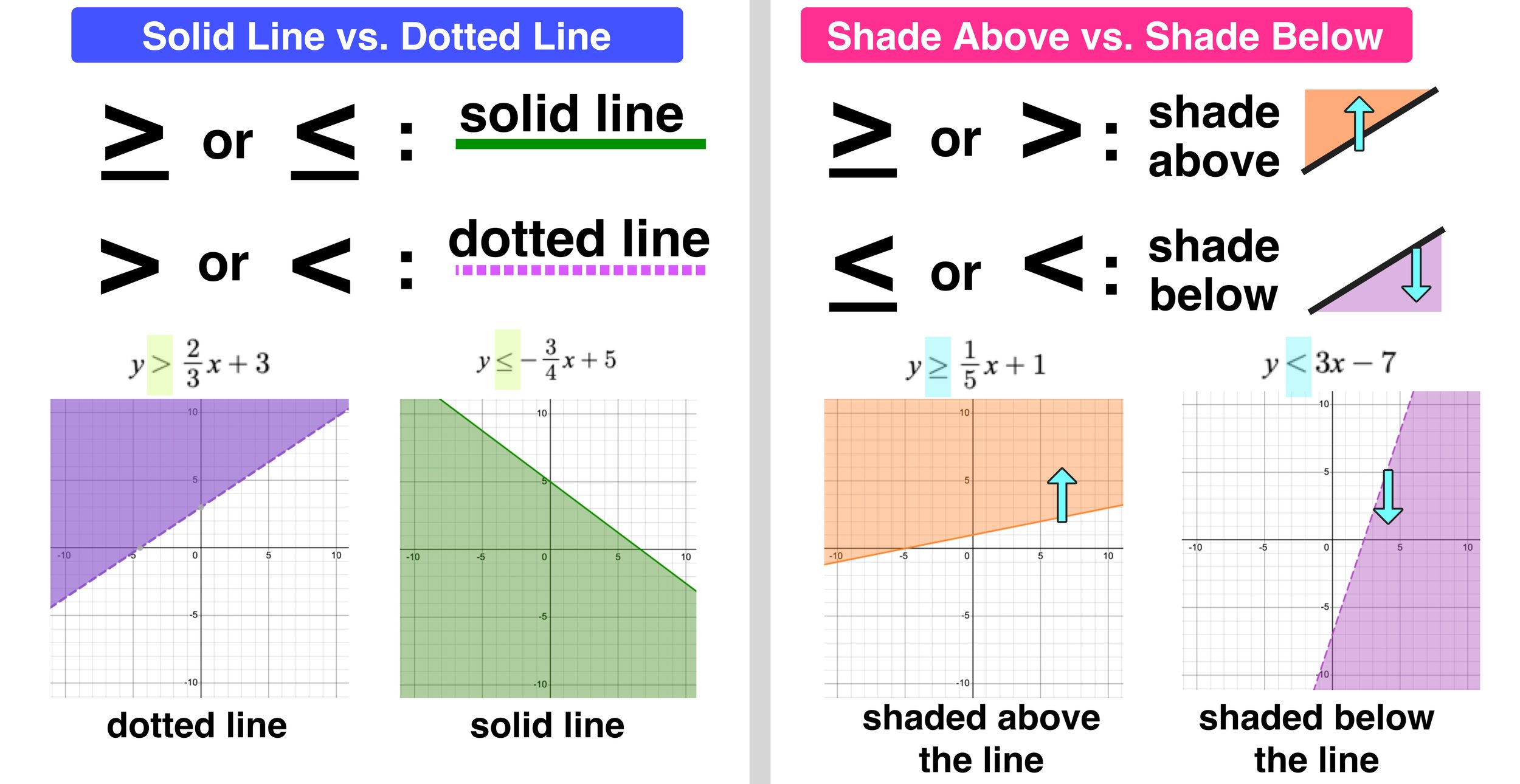
Graphing Linear Inequalities in 3 Easy Steps — Mashup Math
Graphing Linear Inequalities in 3 Easy Steps — Mashup Math
Systems Of Inequalities Calculator
On The Basis Of This Definition, We Can Prove Various Theorems About Inequalities.
An Inequality Is A Mathematical Statement That Compares Two Expressions Using The Ideas Of Greater Than Or Less Than.
How To Solve And Graph A Polynomial Inequality Including Compound, Quadratic, Absolute Value, And Rational Inequalities With Examples.
Learn The Process Of Solving Different Types Of Inequalities Like Linear.
Related Post: